Introduction
The concept of the alternating series error bound is crucial in the realm of calculus and analysis, providing a way to estimate the error in the partial sums of alternating series. This mathematical principle is not only fundamental in academic studies but also essential in various engineering and science applications. This blog post explores the alternating series error bound in detail, offering insights into its practical applications and calculation methods.
Alternating Series
Before diving into the alternating series error bound, it is important to understand what constitutes an alternating series. An alternating series is a series where the terms alternate in sign. This characteristic leads to a unique behavior in convergence and error estimation, which is where the alternating series error bound becomes particularly useful.
The Basics of the Alternating Series Error Bound
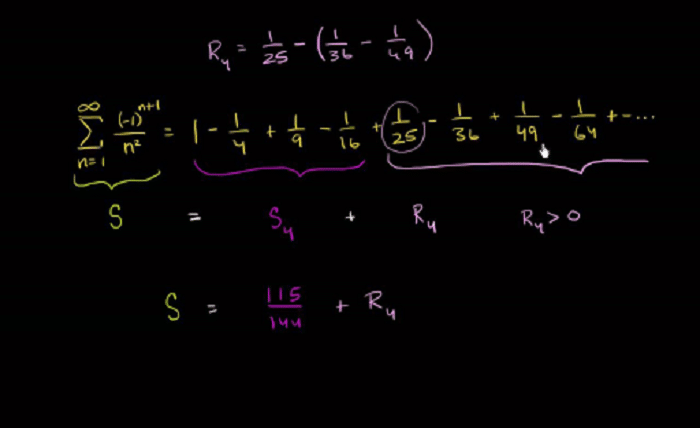
The alternating series error bound provides a method to estimate the error when a convergent alternating series is truncated after a finite number of terms. According to this theorem, the absolute error is less than the first omitted term. This fundamental understanding is crucial for applying the alternating series error bound in practical scenarios.
How to Calculate the Alternating Series Error Bound
Calculating the alternating series error bound involves identifying the first omitted term in the series after truncation. The error bound is then straightforwardly the absolute value of this term, providing a simple yet powerful tool for error estimation in alternating series.
Practical Applications of the Alternating Series Error Bound
The alternating series error bound finds applications in various fields such as numerical analysis, physics, and engineering. Whether it’s in calculating the error in Fourier series approximations or in the numerical solutions of differential equations, the alternating series error bound serves as an essential tool for scientists and engineers.
Examples of Alternating Series Error Bound in Use
To illustrate the use of the alternating series error bound, consider examples from both theoretical mathematics and practical engineering problems. These examples help clarify how the alternating series error bound can be applied to predict and control errors in real-world situations.
Advantages of Using the Alternating Series Error Bound
The primary advantage of using the alternating series error bound is its simplicity and reliability. It provides a clear and conservative estimate of the error, which is invaluable in ensuring the accuracy of calculations and simulations in various scientific and engineering disciplines.
Limitations and Considerations
While the alternating series error bound is highly useful, it has its limitations. Understanding these limitations is important to avoid misapplication of the bound in cases where it might not provide accurate or relevant error estimates.
Comparing Alternating Series Error Bound with Other Error Estimation Techniques
To fully appreciate the utility of the alternating series error bound, it’s beneficial to compare it with other error estimation techniques, such as those used in non-alternating series or in numerical methods that approximate functions and integrals.
Advanced Topics in Alternating Series Error Bound
For those interested in deeper mathematical insights, exploring advanced topics related to the alternating series error bound, such as its derivations and proofs, can provide a more thorough understanding of the underlying principles and their implications.
Conclusion
The alternating series error bound is a fundamental tool in mathematical analysis, offering a straightforward and effective method for estimating errors in alternating series. Whether used in academic settings or applied fields, understanding and applying the alternating series error bound is essential for anyone dealing with series approximations.
FAQs
1. What is an alternating series? An alternating series is a series where successive terms are of opposite signs, which often converges differently compared to non-alternating series.
2. How accurate is the alternating series error bound? The alternating series error bound provides a maximum error estimate, ensuring that the actual error is less than or equal to the bound provided.
3. Can the alternating series error bound be applied to any series? It is specifically applicable to convergent alternating series that satisfy certain conditions outlined in the theorem.
4. What are some common mistakes when using the alternating series error bound? Common mistakes include applying it to non-alternating series or ignoring the conditions under which the series must converge.
5. How can one learn to apply the alternating series error bound effectively? Understanding the theory behind series convergence and practicing with various examples are effective ways to master the application of the alternating series error bound.